
| 小时候,我就在很多科普书上看到过开普勒三定律,包括一些百科全书、从一到无穷大、天文爱好者杂志等等。这三定律是开普勒用第谷在汶岛天文观测的数据总结计算出来的。这三定律加快了日心说击败地心说,还是牛顿引力定律、平方反比定律、角动量守恒的源头,在科学史上意义巨大。开普勒视力不是很好,但是数学能力超群,他小时候与大彗星的相遇让他成了天文学家,他曾经有正多面体宇宙观,后来又计算出了开普勒三定律,也算是几何宇宙观的早期人物之一了,有人认为他毒死了第谷去获得数据,目前人们的验尸已经证伪了这一点,第谷真的是被尿憋死的,只要生病,活人真能让尿憋死。开普勒三定律包括开普勒第一定律(椭圆定律/轨道定律)、开普勒第二定律(面积定律)、开普勒第三定律(周期定律/调和定律),分别是行星(小行星、彗星、卫星等)沿椭圆/抛物线/双曲线轨道(圆锥曲线轨道)运行,中心天体(恒星、行星等)在一个焦点上;行星与中心天体的连线单位时间扫过的面积一定;以及轨道半长轴的立方与轨道周期的平方成正比。小时候我看起来越来越难懂了,直到后来学了更多…… 开普勒第三定律 对于开普勒第三定律,公式是这样的:$$\frac{a^3}{T^2}=K$$ 要想推出受力的公式,可以取一个特殊点,而这个点可以推出一般性的结论。 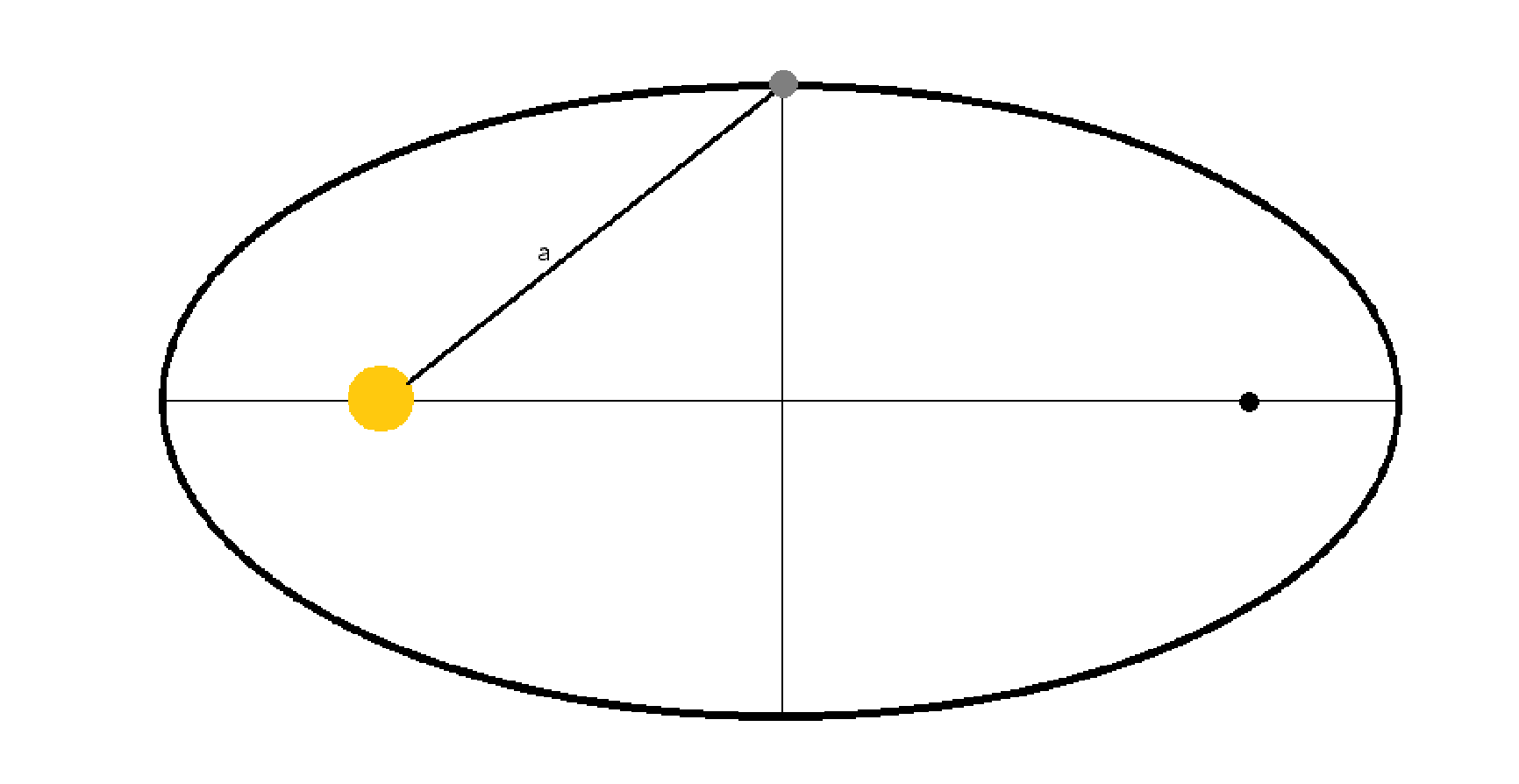 这个点位于短轴与轨道焦点,速度正好是平均速度,角速度也是平均角速度\(\bar{\omega}=\frac{T}{2\pi}\)。因为整体上是一个环绕运动,所以平均受力也是这一点的向心力。$$\bar{F}=m\tfrac{4\pi^{2}}{T^{2}}a$$ 对开普勒第三定律变形,得到\(\frac{a}{T^{2}}=\frac{K}{a^{2}}\),代人上式,得到:$$\bar{F}=\frac{m}{a^{2}}\frac{4\pi^{2}}{K}$$ 把半长轴a换成距离r,同时利用受力对称,两个天体都要考虑,得到:$$F\propto\frac{Mm}{r^{2}}$$ 引入系数G:$$F=G\frac{Mm}{r^{2}}$$ 引力指向中心天体,一般让向外是正方向,得到:$$\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{F}}=-G\frac{Mm}{r^{2}}\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{\hat{r}}}=-G\frac{Mm}{r^{3}}\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{r}}$$ 这是高中的知识,不难理解,不是难点。虽然描述抽象了一点,但不难算。这个比例也和G的量纲有关,是\([L^{3}MT^{-2}]\)。还有这是第一个发现的平方反比定律,平方反比定律是因为我们在三维空间中,能量/场/粒子等在扩散中总量不变,但应为三维球的面积是\(S=4\pi r^{2}\),所以随着膨胀,表面积越来越大,能量/场/粒子被分散开,面积越大分得越散,也就与面积成反比,与距离的平方呈反比。 开普勒第二定律 开普勒第二定律相对难一点,需要入门级微积分。 对于面积,在极短时间dt内,走过距离是vdt,所以扫过的面积是\({\rm d}\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{S}}=\frac{1}{2}\buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{r}\times\buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{v}{\rm d}t\) , 单位时间扫过的面积,也就是面积速度是 $$ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{V}=\frac{{\rm{d}}\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over {S} }}{{\rm{d}}t}=\frac{1}{2} \mathord{\buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{r}}\mathord{\times} \mathord{\buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{v}} $$ 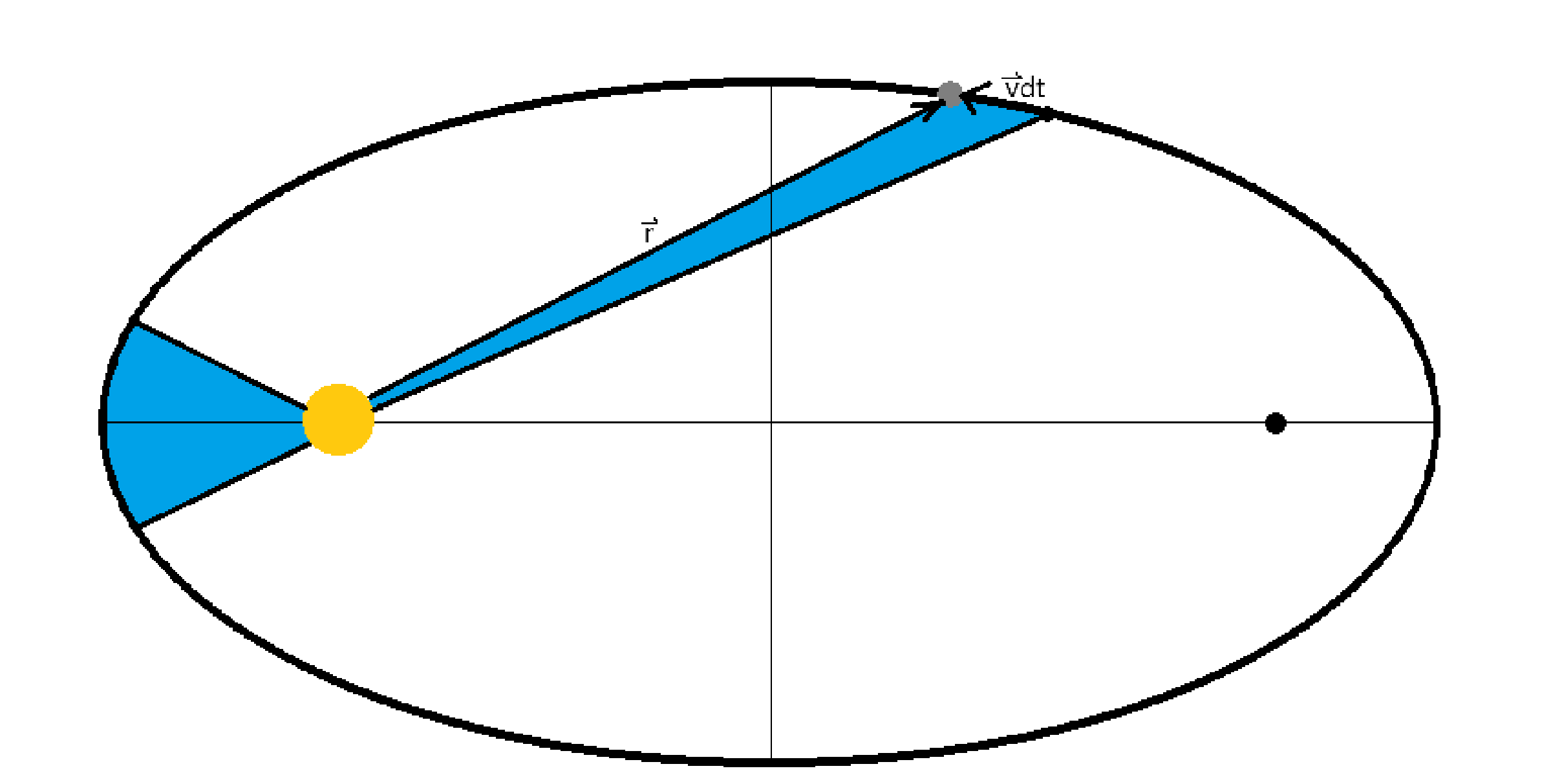 人们通过类比动量\({\rm{\Delta}}\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{p}}=\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{I}=\int \mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{F}}}\mathord{{\rm d}t}\)、\(\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{p}}=m\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{v}}\),发现了角动量\({\rm{\Delta}}\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{L}}=\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{\mu}=\int \mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{M}}}\mathord{{\rm d}t}=\int\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{r}}\mathord{\times}\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{F}}\mathord{{\rm d}t}\)、\(\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{L}}=\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \longleftrightarrow $}} \over{J}}\mathord{\cdot}\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{\omega}}=J\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{\omega}}=mr^{2}\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{\omega}}\)。 可以发现,\(\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{V}}=\frac{\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{L}}}{2m}\),这就是角动量守恒的发现。 因为开普勒第二定律,所以地球轨道速度并不匀速。过近日点一月,过远日点在七月,所以所以冬天太阳更大一点,但不是很明显,地球轨道不是很扁。因为不匀速的运动,导致了日行迹是8字形,每天同一时间拍一张太阳照片,叠加在一起,是一个8字形。可以看到日行迹中太阳最高点和最低点不是8字的顶点,这就是一年中天黑的最早不是冬至,天亮的最早的不是夏至的原因。  小时候,我在想,如果闰正月,是不是就能过两次年了?如果闰腊月,是不是就有两次除夕了?小孩普遍比较盼着过年,但是从小到大从没有遇到过闰正月、闰腊月,这些也就不知道了。闰月,是为了解决阴历与阳历不同步的问题,12个回归月比1回归年要短。闰月的依据是24节气,其中有12个节,分别是立春、惊蛰、清明、立夏 、芒种、小暑、立秋、白露、寒露、立冬、大雪、小寒,12个气,分别是雨水、春分、谷雨、小满、夏至、大暑、处暑、秋分、霜降、小雪、冬至、大寒,这24个节气对应着24个节气点,位于天球上的黄道上,以及地球轨道上。闰月的规则是“无中气置闰”,一个回归月中没有气,那这个月就是闰月,名字是“闰+上个月”。因为24节气在黄道上是等分的,所以地球越快,一个回归月内通过的距离越长,投影到天球上就是太阳在黄道上运行距离更长,也就更容易遇到气点,不容易成为闰月。因为地球的椭圆轨道,所以正月、腊月地球比较快,闰正月、闰腊月也就难以见到了,人们说,“千年难遇闰腊月”。对于相对常见的闰正月,上一次闰正月是1556年(平气1640年),据计算下一次闰正月应该是2262年,已经很遥远了,对于闰腊月,上一次闰腊月是1403年(平气1574年),据计算下一次闰腊月应该是3358年,我们应该都不在了,我们真的不知道这些了。 开普勒第一定律 开普勒第一定律听起来简单,但计算不简单。 首先,要知道椭圆/圆锥曲线的方程,在极坐标下容易理解、计算。如图,利用余弦定理\(r^{2}+(2c)^{2}-2\cdot(2c)\cdot r\cos\theta=(2a-r)^{2}\),展开平方整理得到\(c^{2}-cr\cos\theta=a^{2}-ar\),运用偏心率\(e=\frac{c}{a}\),半通径\(p=\frac{b^{2}}{a}\),得到方程\(r(1-e\cos\theta)=p\)。 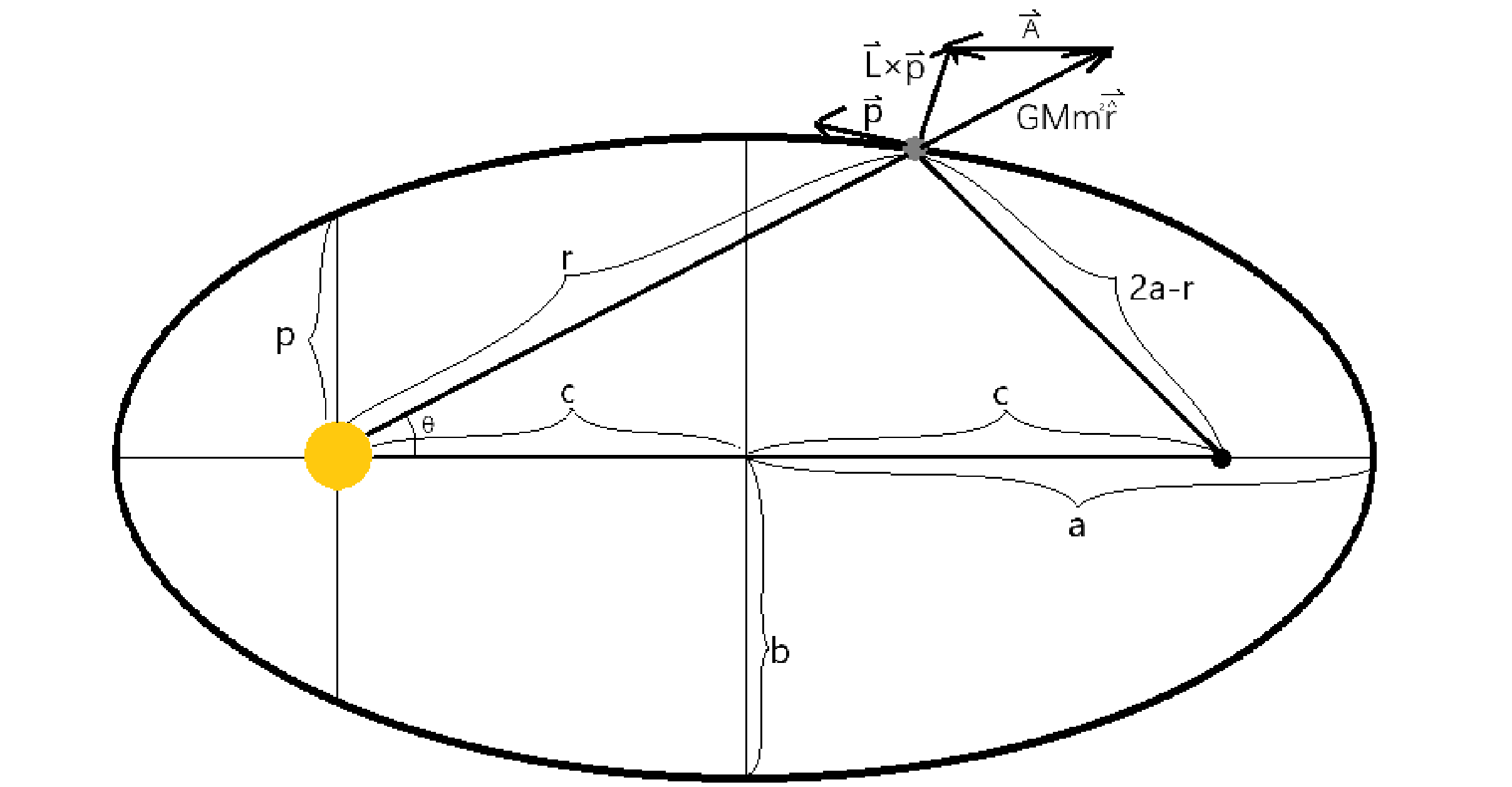 一种方法是利用拉普拉斯-龙格-楞次(LRL)矢量\(\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{A}}=\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{L}}{\times}\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{p}}+GMm^2\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{\hat{r}}}\)。这个矢量是守恒的,对时间求导可以证明。$$\frac{{\rm d}\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{A}}}{{\rm d}t}= \frac{{\rm d}(\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{L}}{\times}\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{p}})}{{\rm d}t}+\frac{{\rm d}(GMm^2\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{\hat{r}}})}{{\rm d}t}$$ $$= \mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{L}}{\times}\frac{{\rm d}\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{p}}}{{\rm d}t}+GMm^2\frac{{\rm d}\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{\hat{r}}}}{{\rm d}t}$$ $$= \mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{L}}{\times}\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{F}}+GMm^2\frac{{\rm d}}{{\rm d}t}\frac{\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{r}}}{r}$$ $$= \mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{L}}{\times}\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{F}}+\frac{GMm^2}{r}\frac{{\rm d}\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{r}}}{{\rm d}t}+GMm^2\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{r}}\frac{{\rm d}(\frac{1}{r})}{{\rm d}t}$$ $$= \mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{L}}{\times}\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{F}}+\frac{GMm^2}{r}\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{v}}-\frac{GMm^2}{r^2}\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{r}}\frac{{\rm d}r}{{\rm d}t}$$ $$= \mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{L}}{\times}\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{F}}+\frac{GMm^2}{r}\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{v}}-\frac{GMm^2}{r^2}\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{r}}v_{r}$$ $$= \mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{L}}{\times}\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{F}}+\frac{GMm^2}{r}\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{v}}-\frac{GMm^2}{r^3}\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{r}}(\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{v}\cdot\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{r}}})$$ 运用万有引力定律,得:$$\frac{{\rm d}\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{A}}}{{\rm d}t}= \mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{L}}{\times}(\frac{GMm}{r^{3}}\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{r}})+\frac{GMm^2}{r}\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{v}}-\frac{GMm^2}{r^3}\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{r}}(\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{v}\cdot\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{r}}})$$ 用速度和距离表示角动量:$$\frac{{\rm d}\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{A}}}{{\rm d}t}= (\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{r}}\times m\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{v}}){\times}(\frac{GMm}{r^{3}}\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{r}})+\frac{GMm^2}{r}\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{v}}-\frac{GMm^2}{r^{3}}\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{r}}(\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{v}\cdot\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{r}}})$$ $$= \frac{GMm^{2}}{r^{3}}(\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{r}}\times\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{v}}){\times}\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{r}}+\frac{GMm^2}{r}\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{v}}-\frac{GMm^2}{r^{3}}\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{r}}(\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{v}\cdot\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{r}}})$$ 运用叉乘的性质\((\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{r}}\times\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{v}}){\times}\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{r}}=\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{r}}(\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{v}\cdot\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{r}}})-\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{r}}^2\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{v}}\),得到:$$\frac{{\rm d}\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{A}}}{{\rm d}t}= \frac{GMm^{2}}{r^{3}}[\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{r}}(\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{v}\cdot\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{r}}})-\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{r}}^2\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{v}}]+\frac{GMm^2}{r}\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{v}}-\frac{GMm^2}{r^{3}}\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{r}}(\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{v}\cdot\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{r}}})=\mathbf{0}$$ 证明了拉普拉斯-龙格-楞次矢量守恒,就可以证明开普勒第一定律。用距离点乘拉普拉斯-龙格-楞次矢量:$$ \mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup $ }} \over{A}} \cdot \mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup $ }} \over{r}} =\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup $}} \over{L}}{\times} \mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup $}} \over{p}} \cdot \mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup $}} \over{r}} +GMm^2 \mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup $ }} \over{ \hat{r}}} \cdot \mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup $ }} \over{r} } $$ $$ = \mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{L}} {\times} \mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{p}}\cdot\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{r}}+GMm^2r $$ 向量的混合积就是所夹的平行六面体的体积,也就是底面积(叉乘)乘高(点乘),正负符合右手定则。在符合右手定则的条件下可以轮换,得到:$$\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{A}}\cdot\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{r}}=\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{p}}{\times}\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{r}}\cdot\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{L}}+GMm^2r$$ $$=-\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{r}}{\times}\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{p}}\cdot\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{L}}+GMm^2r$$ $$=-L^2+GMm^2r$$ 取拉普拉斯-龙格-楞次矢量指向r负半轴,运用内错角相等,整理,得:$$\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{A}}\cdot\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{r}}=Ar\cos\theta=-L^2+GMm^2r$$ $$L^2=r(GMm^2r-A\cos\theta)$$ $$\frac{L^2}{GMm^2}=r(1-\frac{A}{GMm^2}\cos\theta)$$ $$e = \frac{A}{GMm^2},p = \frac{L^2}{GMm^2} $$ Q.E.D. 另一种方法是微分方程。把角动量公式变形\(\omega=\frac{L}{J}=\frac{L}{mr^2}=\frac{LR^2}{m}\),R是r的倒数类似曲率。可以算出径向速度:$$v_r=\frac{{\rm d}r}{{\rm d}t}=\frac{{\rm d}\theta}{{\rm d}t}\frac{{\rm d}r}{{\rm d}\theta}=\omega\frac{{\rm d}r}{{\rm d}\theta}=\frac{LR^2}{m}\frac{{\rm d}\frac{1}{R}}{{\rm d}\theta}=\frac{LR^2}{m}(-\frac{1}{R^2})\frac{{\rm d}R}{{\rm d}\theta}=-\frac{L}{m}\frac{{\rm d}R}{{\rm d}\theta}$$ 从而算出径向加速度:$$a_r=\frac{{\rm d}v}{{\rm d}t}=\frac{{\rm d}\theta}{{\rm d}t}\frac{{\rm d}v}{{\rm d}\theta}=\omega\frac{{\rm d}v}{{\rm d}\theta}=\frac{LR^2}{m}\frac{{\rm d}}{{\rm d}\theta}(-\frac{L}{m}\frac{{\rm d}R}{{\rm d}\theta})=-\frac{L^2R^2}{m^2}\frac{{\rm d^2}R}{{\rm d}\theta^2}$$ 列出加速度平衡公式:$$a_引=a_r-a_向$$ $$-\frac{GM}{r^2}=-\frac{L^2R^2}{m^2}\frac{{\rm d^2}R}{{\rm d}\theta^2}-\omega^2r$$ $$-GMR^2=-\frac{L^2R^2}{m^2}\frac{{\rm d^2}R}{{\rm d}\theta^2}-(\frac{LR^2}{m})^2\frac{1}{R}$$ $$-GMR^2=-\frac{L^2R^2}{m^2}\frac{{\rm d^2}R}{{\rm d}\theta^2}-\frac{L^2R^3}{m^2}$$ 整理,得:$$\frac{GMm^2}{L^2}=\frac{{\rm d^2}R}{{\rm d}\theta^2}+R$$ $$\frac{{\rm d^2}{(R-\frac{GMm^2}{L^2}})}{{\rm d}\theta^2}+R-\frac{GMm^2}{L^2}=0$$ 求解微分方程,消掉\(R-\frac{GMm^2}{L^2}\),特征方程是\(\frac{{\rm d^2}}{{\rm d}\theta^2}+1=0\),\(D^2+1=0\),解为\(D=\pm i\),得到微分式\(D(R-\frac{GMm^2}{L^2})=\pm i(R-\frac{GMm^2}{L^2})=\frac{{\rm d}}{{\rm d}\theta}(R-\frac{GMm^2}{L^2})\)。积分上式得:$$\int\pm i{\rm d}\theta +C=\int\frac{{\rm d}(R-\frac{GMm^2}{L^2})}{R-\frac{GMm^2}{L^2}}$$ $$\pm i\theta +C=\ln(R-\frac{GMm^2}{L^2})$$ $$R-\frac{GMm^2}{L^2}=e^{\pm i\theta+C}=e^C(\cos\theta+i\sin\theta)$$ 取实数部分:$$R=e^C\cos\theta+\frac{GMm^2}{L^2}$$ 得出:$$\frac{L^2}{GMm^2}=r(\frac{L^2e^C}{GMm^2}\cos\theta+1)$$ $$e=\frac{L^2e^C}{GMm^2},p=\frac{L^2}{GMm^2}$$ Q.E.D. 还有一种方法,是在b站上3bule1brown讲的。 首先,利用圆的离心点的性质构造椭圆。 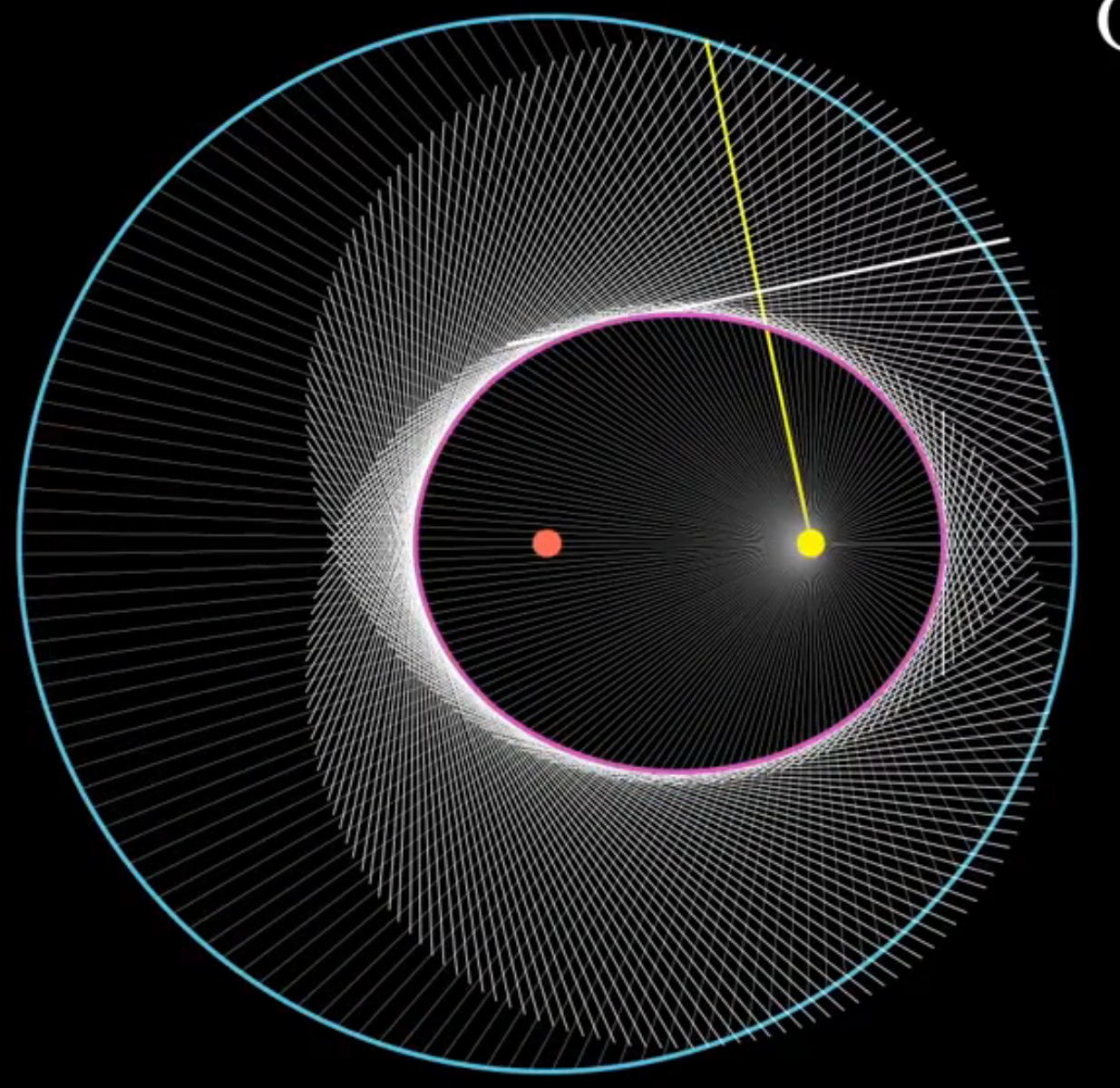 然后,用开普勒第二定律获得速度空间。  最后,把速度空间与轨道通过离心点联系起来。 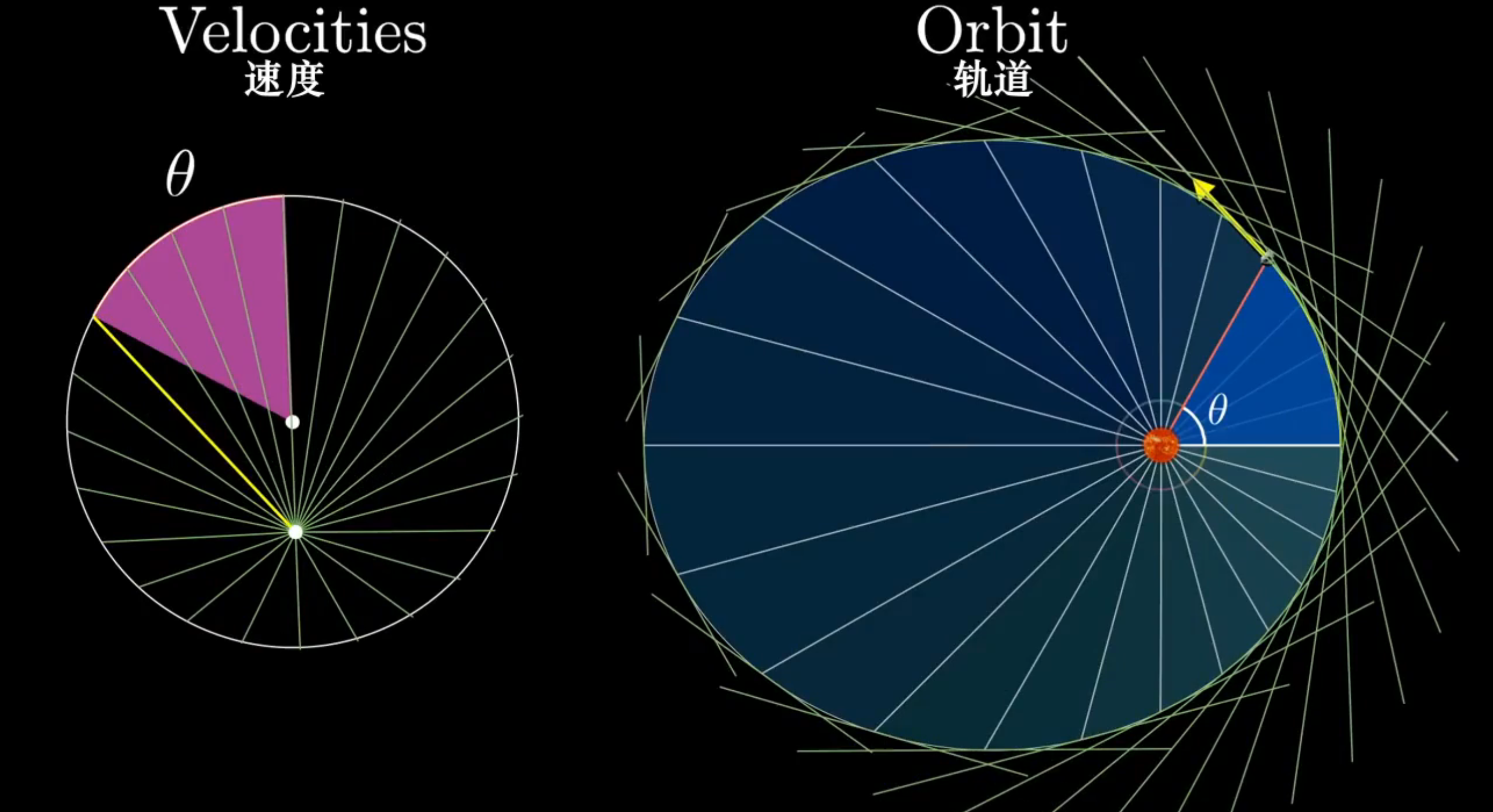 还有,要想求出具体的离心率,还需要进一步计算。 首先,是计算半通径,运用角动量:$$\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{L}}=\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{r}}\times\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{p}}=\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{r}}\times m\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{v}}=2m(\frac{1}{2}\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{r}}\times\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{v}})=2m\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{V}}$$ 取平均值:$$L=2m\bar{V}=2m\frac{S}{T}=2m\frac{\pi ab}{T}$$ 平方,得到:$$L^2=\frac{4\pi ^2m^2a^2b^2}{T^2}$$ $$b^2=\frac{L^2T^2}{4\pi ^2m^2a^2}$$ 运用开普勒第三定律\(\frac{a^3}{T^2}=\frac{GM}{4\pi^2}\),做比,得到:$$p=\frac{b^2}{a}=\frac{L^2}{GMm^2}$$ 与解出的结果一致。 运用引力势能:$$E=\int_{r}^{+\infty} -\frac{GMm}{r^2}\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{\hat{r}}}\cdot{\rm d}\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over{r}}=-\frac{GMm}{r}$$ 取r=a特殊点,利用速度为平均速度且速度方向与圆心到天体距离垂直,得到:$$ E = E_k + E_p = \frac{1}{2} mv^2- \frac{GMm}{a} = \frac{1}{2} m \bar{v}^2 - \frac{GMm}{a} = \frac{a}{2} \frac{GMm}{a^2} - \frac{GMm}{a}= - \frac{GMm}{2a}$$ 做比,得到: $$ \frac{b^2}{a^2} = - \frac{2EL^2}{G^2M^2m^3 }$$ 可以求出偏心率:$$e^2 = \frac{c^2}{a^2} = \frac{a^2-b^2}{a^2} =1- \frac{b^2}{a^2} =1+ \frac{2EL^2}{G^2M^2m^3} $$ $$e = \sqrt{1+ \frac{2EL^2}{G^2M^2m^3}}$$ 可以看出来,在圆周运动时\(E=\frac{1}{2}mv^2-\frac{GMm}{r}=\frac{r}{2}\frac{mv^2}{r}-\frac{GMm}{r}=\frac{r}{2}\frac{GMm}{r^2}-\frac{GMm}{r}=-\frac{GMm}{2r}\),算出\(e=\sqrt{1+\frac{-\frac{GMm}{2r}2L^2}{G^2M^2m^3}}=\sqrt{1-\frac{L^2}{GMm^2r}}=\sqrt{1-\frac{(mvr)^2}{GMm^2r}}=\sqrt{1-\frac{r^2}{GMmr}\frac{mv^2}{r}}=0\),结果正确,轨道是圆,E=0时,是逃逸速度,无穷远处动能完全转化为势能,算出e=1,是抛物线。速度在两者之间,0<e<1,是椭圆。速度更大,e>1,是双曲线。 后记 开普勒三定律事实上难度是开普勒第一定律最难,开普勒第二定律中间,开普勒第三定律最简单。这与小时候的想法完全是反的。不得不说宇宙有很大的欺骗性,这是个有趣的问题。这篇文章是一篇类似笔记的东西,希望对大家能有帮助。 |